目次
STDEV 関数
STDEV 関数は、引数を母集団の標本であると見なします。 指定する数値が母集団全体である場合は、STDEVP 関数を使用して標準偏差を計算します。
標準偏差は、n-1 法を使って計算されます。 引数には、数値、数値配列、または数値を含む範囲を参照する名前かセル参照を指定します。
=STDEV(数値 1,[数値 2],[数値 3],[数値 4]…)
標準偏差とは?
データや確率変数の散らばり具合(ばらつき)を表す数値のひとつ。
例えば、ある試験でクラス全員が同じ点数、すなわち全員が平均値の場合、データにはばらつきがないので、標準偏差は 0 になります。
使用例

この場合、標準偏差は「34.64」となります。

平均値
平均の場合…
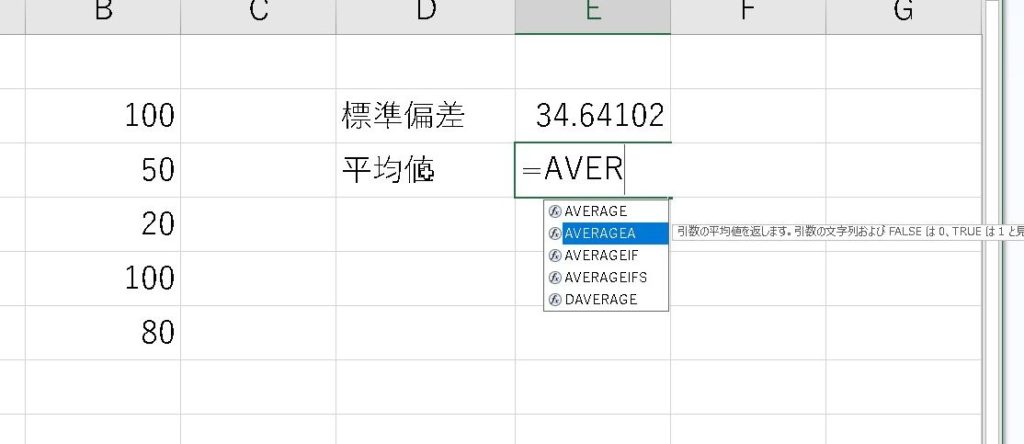
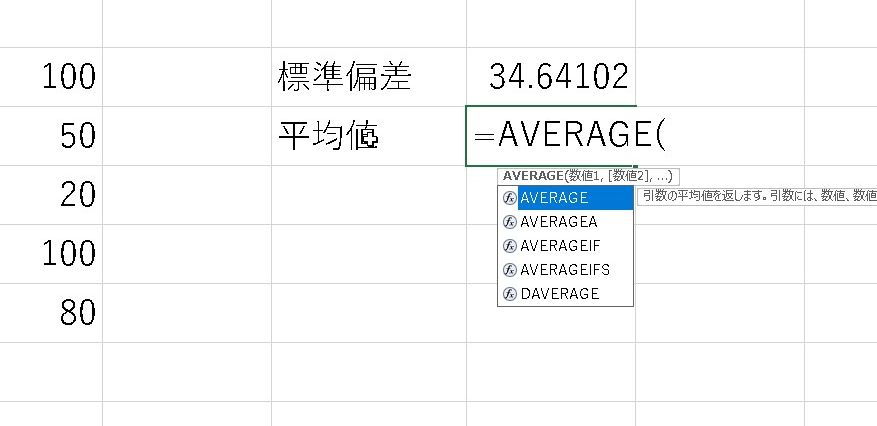

平均値は「70」となります。
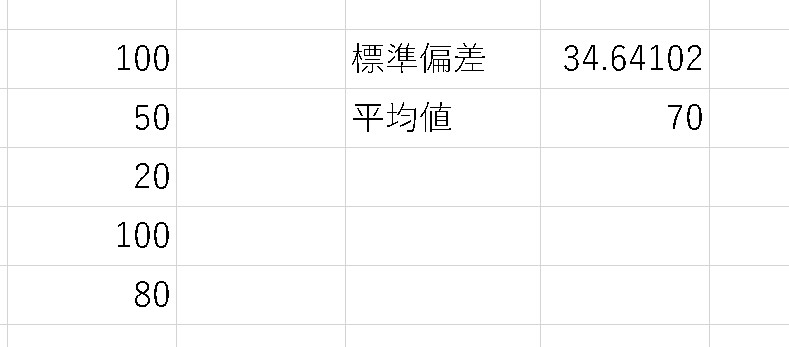
偏差と平均は違う
偏差とは「データや確率変数の散らばり具合(ばらつき)を表す数値」
平均とは「数の集合の中間的な値のこと」
平均値だけ見ると危ない
例えば、6名の生徒が居て、100点を取った生徒が3名、0点を取った生徒が3名の場合、平均点を見ると「50点」となってしまい、(50点を取った生徒は1人も居ないはずなので)ちょっと違和感が出ます。
標準偏差を取ると「54.77」となり、全体が、中央値から「54.77」程度離れている、ということがわかります。
50点を取った生徒が6名の場合は、平均点「50点」標準偏差「0」となるので、この集団は全員が中央値を取っている平均的な集団である、ということがわかります。
全体の点数が中央値からどの程度ばらつきがあるのか?という数字を見る時は「平均」ではなく「標準偏差」を見るようにしましょう!
ご参考下さい(^o^)/