DCF法の残存価値計算で出てくるひとつが「無限等比級数の和の公式」です。※無限等比級数は高校数学Ⅲで出てくる公式のようです。
無限等比級数とは?
無限等比級数とは、公比が一定である等比数列の無限和を指します。それぞれの項が公比q(q≠1)で相互に等しい関係にある数列です。
1/4 , 1/16 , 1/64 , 1/256・・・
このような場合、各項の間に公比があります。a1, a2, a3, …, an, …という数列があるとき、S = a1 + a2q + a3q^2 + … + anq^(n-1) + … と表されます。
無限等比級数の和の公式とは?
無限等比級数の和の公式とは、a1, a2, a3, … の無限等比級数の和を求めるためのものです。
公式は、a1/(1-r) です。
ここで、a1は級数の初項で、rは公比です。ただし、|r| < 1 の場合に限り有効です。
無限等比級数の和の公式例
例えば、下記のような無限等比級数の和があった場合。
1/2+1/4+1/8+1/16+⋯=∞∑(𝑛=1)(1/2)𝑛 = 1
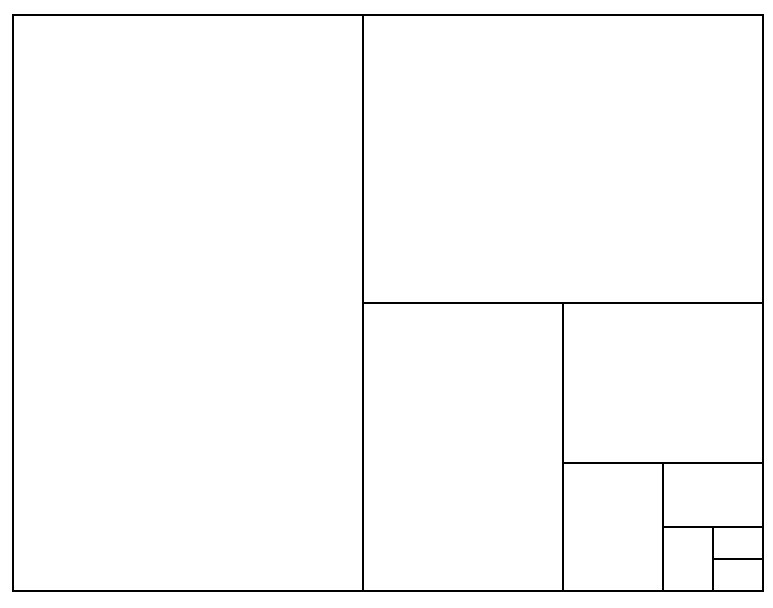
この無限等比級数の和が1になります。
まとめ
まずは、無限等比級数の和の概要についてでした。
次回は、詳しい計算方法などをまとめていきたいと思います。




