目次
ダイクストラ法の概要
ダイクストラ法は、特定の始点から他のすべての頂点への最短経路を見つけるためのアルゴリズムです。辺の重みが非負であることが前提です。
ここでは、ダイクストラ法の手順をひとつずつ詳しく解説し、具体例を用いて説明します。
初期化
まず、始点を選び、その始点からの距離を0に設定します。他のすべての頂点の距離は無限大に設定します。
これは、まだどの頂点にも到達していないことを示しています。
具体例:
- 頂点Aを始点とし、他の頂点B, C, D, Eがあるとします。
- 初期設定: 距離(A) = 0, 距離(B) = ∞, 距離(C) = ∞, 距離(D) = ∞, 距離(E) = ∞
未確定の頂点の選択
次に、まだ確定していない頂点の中から、始点からの距離が最小の頂点を選びます。
この頂点は、現時点で最短経路が確定したものとして扱われます。
具体例:
- 初期状態では、始点Aが最短距離0で確定します。
距離の更新
選ばれた頂点から直接つながっている未確定の頂点に対して、始点からの累積距離を計算します。
既存の値より小さい場合はその距離を更新します。
具体例:
- 頂点AからBへの辺の重みが4、AからCへの辺の重みが2であるとします。
- 距離(B) = min(∞, 距離(A) + 重み(A, B)) = min(∞, 0 + 4) = 4
- 距離(C) = min(∞, 距離(A) + 重み(A, C)) = min(∞, 0 + 2) = 2
繰り返し
すべての頂点の最短距離が確定するまで、未確定の頂点の選択と距離の更新を繰り返します。
具体例:
- 次に、距離が最小のCを選びます。
- Cからつながる頂点の距離を更新します。
- この手順を繰り返し、すべての頂点の最短距離を確定します。
まとめ
ダイクストラ法は、効率的に最短経路を見つけるための強力なアルゴリズムです。非負の重みを持つグラフにおいて、特定の始点から他のすべての頂点への最短経路を求める際に用いられます。
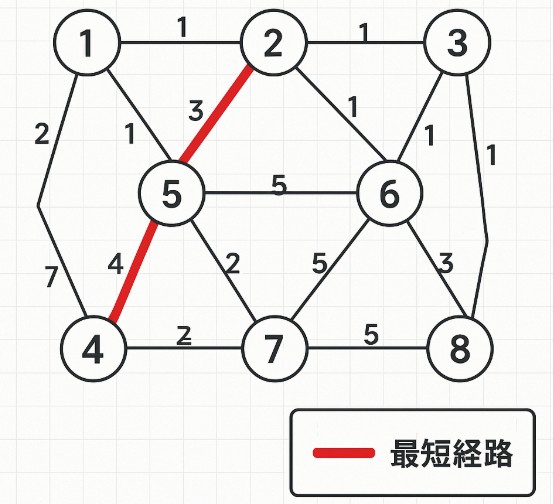
ダイクストラ法は、ネットワークルーティングや交通経路探索など、さまざまな実世界の問題に応用されています。




