モンティ・ホール問題は数学と確率論の分野において有名で議論を巻き起こした問題の一つです。この問題はアメリカのテレビゲームショー「Let’s Make a Deal」にちなんで名付けられ、そのショーのホストであるモンティ・ホールに由来しています。
問題の内容は直感に反する結果を導くことから、多くの人々を驚かせ、議論を呼んできました。
問題の内容
モンティ・ホール問題は以下のように設定されます。
- 参加者の前には3つの閉じたドアがあり、そのうち1つのドアの後ろには車が、残りの2つのドアの後ろにはヤギがそれぞれ隠されています。
- 参加者は最初に1つのドアを選びますが、そのドアはすぐには開けられません。
- モンティ・ホール(ホスト)は参加者が選ばなかったドアの中から1つを開け、必ずヤギがいるドアを選んで見せます。
- その後、参加者には最初に選んだドアを維持するか、残りの閉じたドアに変更するかの選択が与えられます。
ステップバイステップのシナリオ
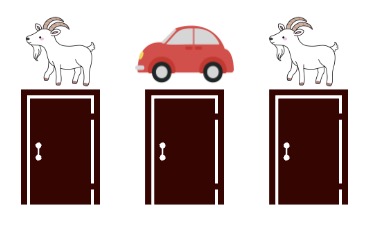
- ゲームのセットアップ: ゲームには3つの閉じたドアがあります。1つのドアの後ろには車があり、残りの2つのドアの後ろにはそれぞれヤギがいます。車とヤギの配置はランダムで、ゲームの始めに参加者はどのドアの後ろに何があるか知ることはできません。
- 参加者の初期選択: 参加者は、3つのドアの中から1つを選びます。この時点で、参加者の選んだドアの後ろに車がある確率は1/3です。なぜなら、3つのドアのうち、ただ1つだけが車の後ろになるからです。
- ホストの行動: モンティ・ホール(ゲームのホスト)は、参加者が選んだドアとは異なる2つのドアのうち、ヤギが後ろにある1つのドアを開けます。ホストは常にヤギが後ろにあるドアを開けるため、参加者の初期選択が車の後ろだった場合、ホストには選択肢がありません。しかし、参加者が最初にヤギの後ろのドアを選んだ場合、ホストは残りのヤギが後ろにあるドアのうち、開けない方を選びます。
- 参加者の最終選択: この時点で、参加者には2つの選択肢があります。最初に選んだドアを維持するか、もう1つのまだ閉じられているドアに変更するかです。
直感と実際の確率
- 最初の選択を維持した場合: 参加者が最初に選んだドアの後ろに車がある確率は、選択時点で1/3です。ホストの行動はこの確率に影響を与えません。したがって、最初の選択を維持する場合の勝利の確率は1/3のままです。
- 選択を変更した場合: 参加者が最初に選んだドアの後ろにヤギがある確率は2/3です(3つのドアのうち2つがヤギです)。ホストがヤギが後ろにあるドアを開けることによって、この2/3の確率が残りの閉じたドアに移ります。つまり、ドアを変更することで、参加者が車を勝ち取る確率は2/3になります。
議論の火付け役
この問題が広く知られるようになったのは、1990年にアメリカの数学者マリリン・ヴォス・サヴァントが「Parade」誌のコラムで問題を取り上げ、ドアを変更することで勝利の確率が高まると解答したことからです。
彼女の解答は多くの読者、特に数学者や科学者からの激しい反論を受けました。しかし、その後の詳細な分析とシミュレーションによって、彼女の解答が正しいことが証明されました。
問題の意義
モンティ・ホール問題は、直感と実際の確率が一致しない例として有名です。この問題を通じて、直感に頼る代わりに数学的な分析の重要性が強調されます。
また、確率論の教育においても、この問題は理解と議論のための興味深いケーススタディとなっています。




